Tensegrity: Mast Concepts

Inevitably exploration of tensegrity progresses to the building of masts or towers. The most common structural unit for building a mast is the T-Prism or 3-Prism.

I have looked at 2 variations of the T-Prism with one having both the base and the top triangular sections formed from the same equal length tension ties and the second with the base tension ties longer than the top tension ties, essentially forming a slightly pyramidal form.

In a tiered mast arrangement the slight variations in form become quite apparent with my preference favouring the second form.

In each case (above) the second tier is an inverted copy of the base form.

Finally, it is the inspiration from one of Kens fine works that has helped me decide on how I will proceed with the mast, technically not a mast but a 2 tier arrangement.

 

The inspiration is from Kenneth Snelsons; Osaka, 1970 stainless steel 32 x 16 x 16 feet Japan Iron & steel Federation, Kobe, Japan.

Tensegrity: Geometrix

Tensegrity geometry involves fairly complex mathematics and it is the work of Robert William Burkhardt,that I continually refer to. A detailed account of his mathematical research and design theory is presented in the publication: A Practical Guide to Tensegrity Design.

In this publication he starts with the most basic of Tensegrity forms the T-Prism also known as 3-Prism.
 
These are just some of the images; captured from his publication; that illustrate his theories.
The mathematics are well documented but are too complex to discuss in detail here. He also covers how to adapt the formulae depending on what parameters are sought or known.

A recommended read for anyone interested in Tensegrity structures.
I would like to explore an alternative geometrix theory for this basic form of Tensegrity. If we consider a number of factors relating to this form, we find that for all compressive struts being equal in length the top triangular plane is parallel to the bottom triangular plane. We also know that for any given situation the rotational symmetry; that is the rotation about the centre axis (z-axis in above); has limitations due to the length of the struts assuming a fixed point at the base.

Essentially if we take the static vertical arrangement as per the first illustration above and rotate the top triangular form we reach this limitation at approx 180 degrees or the perceived point of intersection of all 3 struts.
 
These illustrations are from my own work with the first one showing the final 3 Prism arrangement and the second showing the theoretical graphical geometry for determining the location and size of the vertical tension members.
What I have done is create 2 circles defining the perimeter transcribed by the rotational movement assuming a fixed point at the base. The top circle is located at the strut length fully vertical with the lower one at the elevation on the point of maximum rotation. The path of movement from the vertical position to the maximum rotational symmetry achievable is shown as the Radial Path.

The radial path is determined by plotting a series of points at intervals tracking the motion of the strut from the vertical position. This path is transcribed on the perimeter surface of the 2 projected circles. This path passes beyond the minimum distance between the rotated strut and the eventual base point that would be connected by a tension strut.
So using the measuring capabilities of Solidworks it is simply a case of selecting the Radial Path and the associated connecting point at the base to determine the minimum dimension and thus we derive the ideal tension member length.
My findings at this stage are theoretical and I still need to prove the results with further experimentation. In this case I compared my theory with the model created using a dataset conceived by Robert William Burkhardt and there was a variation of only 0.04mm.
This variation may be attributed to the spline created from the series of points defining the radial path. The interpolation of this spline is dependant on the number of points (6) selected and consequently proportionally accurate.

Tensegrity Concept Models

When developing CAD models I often consider how I would go about actually building a physical representation of the design I see before me on screen.

I wanted to use readily available material in such a manner as to provide good compression resistance for the struts and minimum expansion (stretch) for the tendons.

Naturally I spent some time browsing the Internet to see what others were doing in the construction of their models. The majority of models comprised a simple sturdy strut connected to the tendons by either a screw at the end or tied. The tendons in most cases were either string or fishing line.

I quite liked the idea of using fishing line for the tendons and decided that utilising crimps would be ideal to form a connection to the end of the struts.
For the struts I decided on a composite material approach as shown in the following images.



The image on the left is a composite construction comprising thin dowel restrained along its length by beads. The dowel on its own is ineffective as a compression member but when constrained by a series of close fitting beads this becomes an effective solution. This could be further improved by using hollow spacers, either aluminium or steel with flat ends thus increasing the contact surface area. The dowel in this case keeps the "beads" together and forms a projection at the end of the strut to which we can simply hook on the tendons as shown in the left or simply act as a shaft to constrain washers to which we in turn fit the tendons (right image).

The image on the right is similarly a composite construction but this time the dowel is fitted with a close fitting sheath of plastic pipe. Again an effective solution with the ends of the pipe forming an edge to prevent the washers slipping down the strut.

Composite construction techniques provide a good alternative to the traditional approach of building tensegrity models. The idea that the selected materials provide restraint to the compression strut as well as acting as a contact surface for attaching the tendons without the need to use screws works very well.

Recently my work was featured in the Tensegity Wiki.
Tensegrity Wiki link: http://tensegritywiki.blogspot.com
If you would like more technical information or have a general enquiry please drop me a line at hught2008@gmail.com

Tensegrity Modelling: Design Considerations

Tensegrity structures are distinguished by the way forces are distributed within them.
The members of a tensegrity structure are either in tension or in compression. For the structures I have so far researched; that have been done by others; the tensile members are usually cables or rods, while the compression members are sections of tubing, pipe or rods.

For the tension members I have decided to work with mono line rated at 30lb or 14kg which satisfies my initial criteria for tension capacity.

Compression Members:

This is my primary focus at this time, as I am keen to evolve the definition of what constitutes an acceptable compression strut for the purpose of tensegrity model making. Something that opens up more opportunity for individual expression and provide additional options. It is very tempting to replicate the fine work of artists like Bruce Hamilton, who has developed a series of extraordinary and very elegant models, but that would not satisfy my curiosity for exploration.

What I doing though is looking at compound construction techniques that utilise materials which normally in isolation are ineffective but in conjunction with other material work well together to form strong compression struts.

Design Considerations:

In engineering, buckling is a failure mode characterized by a sudden failure of a structural member subjected to high compressive stress, where the actual compressive stress at the point of failure is less than the ultimate compressive stresses that the material is capable of withstanding. This mode of failure is also described as failure due to elastic instability. source: Wikipedia

Some brief notes on bending due to compression that is an inherent consideration in respect of developing compound compression struts.

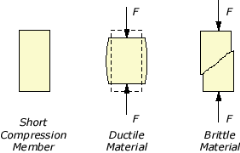Compression members, such as columns, are mainly subjected to axial forces. The failure of a short compression member resulting from the compression axial force looks like:

 

 

However, when a compression member becomes longer, the role of the geometry and stiffness becomes more and more important. For a long (slender) column, buckling occurs well before the normal stress reaches the strength of the column material.

In the case of Tensegrity models the struts replace the column in this instance. The tendency to bend under stress can be managed with compound materials and hence satisfy the conditions for structural strength.

Thus the purpose of my research is simply to explore these options.

For more specific details on bending under stress and slenderness ratio with some very good graphics on this subject I would suggest:

http://sites.google.com/site/simeonlapinbleu/tensegrity

Tensegrity 3d Cad Model Gallery:

 

 

 

 

3d Cad: Tetrahedron Tensegrity 3v.

This is my first 3D Cad Tensegrity model, technically described as a 3v Pars Tetra Tensegrity.

This design is actually not from the Bucky Fuller stable or indeed from Kenneth Snelson, instead it is devised by a very clever fellow called Marcelo Pars, who has done extensive work with tensegrity structures. I only recently came across Marcelos’ work which has opened a whole new understanding of the subject.

The design is based on a data-set created by Bob Burkhardt, who has studied in detail the mathematics of tensegrity structures.

3D CAD is an ideal medium to explore these structures enabling a degree of accuracy that physical models cant achieve. This environment also provides additional visualization tools that can dissect the models to further examine the construction and gain insights into the underlying geometric symmetry.

For all new tensegrity structures I would first develop the design in 3d Cad using where possible available data-sets from various sources. Occasionally where no data-set exists I would simply develop the design from visual inspection.

To fully comprehend the structural form it is absolutely imperative to attain a high degree of accuracy working to approximations will not suffice. It is therefore not unusual to have to work to 4 decimal places to achieve a fully constrained accurate model.

Working with datasets is an ideal starting point but in my experience still requires additional micro adjustment to fully constrain the final model.

Normally the process involves starting with building the struts and tendons as individual parts and laying out a rough shape of the form as an assembly and then constraining each of the individual struts to each node point on the tendons.

However it is very easy for this whole thing to become chaotic as you constrain the struts and occasionally the structure may become unstable as the Cad program will take the shortest route to connect the elements. To negate this and provide some control it is always best to ‘ground’ one component prior to connecting another keeping the items as close as possible to each other before constraining.

When the assembly is complete it is not unusual to find that the model exhibits some flexibility which technically should not be there. Its not because the model is not fully constrained its just that dimensionally struts or tendons are not nearly accurate enough to fully define the model. This is where it gets tedious...in order to achieve the final "fixed" result we need to select a tendon part or strut and micro adjust the dimension of this part to finalise the structure. I should note that selection of a "part" in an assembly will apply the adjustment to all the parts with the same properties (which is exactly what we want).

Once completed we can then begin to explore the model for geometric consistencies and symmetry. 

To prove geometric symmetry and relationships it is necessary to build a number of dimensional variations of the same structure and overlay these in one assembly. In the blog entries to follow I have often demonstrated this principle by showing dimensional variations of one model in the context of proving an observation.

For more information please contact me at hught2008@gmail.com
Bob Burkhardt website: http://bobwb.tripod.com/synergetics/photos/pars.html
Marcelo Pars: http://www.tensegriteit.nl/

Updated: 11th February 2012