Updating Blog Aug 2015

I will be updating some of the images and collections in the existing articles and look at ways of clarifying the inclusion of the virtual elements pertaining to rotational axis and geometrics.
Please bear with me while I sort things out.
Please refer to the tab called “Tensegrity Symmetry” which will explain in detail my objectives.

I was asked if there was a way of clarifying the inclusion of the rotational symmetry and geometric virtual elements as they tend to obscure the actual Tensegrity form. This is something I am looking into but I should note the primary reason for them being modelled instead of just shown as lines is because single sketched lines do not translate well to a 3D PDF.

Tensegrity: Model Files

I have decided to make available a number of viewable 3D model files from the most recent articles relating to Tensegrity Symmetry.

The link will open a page on Google Docs where the file can be downloaded. Each file created is a 3D PDF which can be viewed in the free Adobe Acrobat Reader. The 3D PDF file format allows the user to interact with the model.

Tensegrity 3v Pars Tetra RS




Tensegrity Cube RS




Tensegrity Tetrahedron RS




Tensegrity T-Prism RS



Tensegrity Octahedron RS




Tensegrity Skew Prism Arch



NOTE: “RS” denotes models inclusive of Axis/Rotational Symmetry elements; in each case the brown struts are the actual tensegrity compression struts, the green and purple struts are virtual elements representing the transitional states and the blue struts are virtual elements to represent the axis of symmetry.

When you “activate” a 3D PDF the file opens with a toolbar across the top of the screen. Some of these files may have been processed as perspective views, so to change this to orthographic just select the toolbar button as highlighted above.
Other toolbar features include lighting setups, rotational and preset views, model hierarchy menu and CAD model presentation options.
If you have any questions about use of these files, viewing options or if you have problems accessing the link, then please drop me a line via the Contact page.

The Google Docs is a temporary location until I find something more permanent.

Tensegrity: T-Prism Geometrix

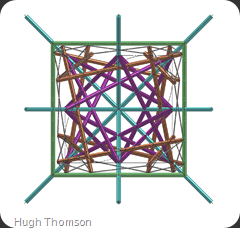
Considering my current research, it was inevitable that I would have to revisit my earlier theories on the construction of the tensegrity T-Prism and have a look at this structure for rotational symmetry.

http://spatialgeometrix.blogspot.com/2010/09/placeholder-geometry.html

My earlier thoughts on the development of this type of tensegrity still hold true, but building a model based on rotational symmetry has greater appeal and simplicity.

 

 

 

If we consider again the parameters of transition of the morphing from one state to another we will see that the green triangle form transitions to a single linear form as shown on the left image.

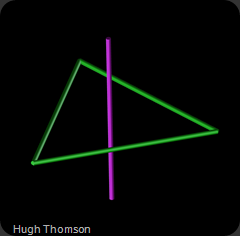
The right image (above) shows the relationship of the green triangular form to the blue struts representing the axis of symmetry. These lines intersect on the midpoints of the green struts.

Now we introduce the T-Prism or 3-Prism structure to this assembly and align it accordingly.

The brown struts are located at the midpoint with the blue axis struts resulting in a balanced arrangement.

To create a tapered T-prism move the intersection point of the brown struts towards one end. In each case the brown struts remain perpendicular to the axis of the blue struts.

The last image shows the parallel relationship of all three planes, assuming a plane connecting the triangular arrangement at the top and bottom of the T-prism.

 

 

The concept of rotational symmetry as discussed in the recent posts here is something I am quite excited about.

I would be interested to receive comments on my ideas and hopefully enter into some discussion with others about tensegrity and rotational symmetry.

So please drop me a line at hught2008@gmail.com

Tensegrity: Cube Geometrix

Rotational/Geometric Symmetry; Slowly progressing thru the range of tensegrity structures I have so far modelled it seemed appropriate to now have a look at the cube!

The tensegrity cube featured here is affectionately referred to by Bob Burkhardt as a Zig-Zag cube, somewhat differentiating it from the Orthogonal variant (not shown). This structure in contrast to its cousin has better stability and not quite so “jiggly”. Thus the reason why I am doing this one and not its cousin!

When I started to look for the geometric symmetry in this model I was puzzled as to how this formation could translate from the green cube to the star linear format (purple) as shown in the next 2 images.

 

In combination (above left) the translation formats do little to clarify the situation.

However when I introduced the cube itself into this geometry model I created a third construction set as a reference to represent the axis of geometric symmetry.

The blue axis of symmetry shown below has a common centre point passing through the centre of each strut. Thus we have the rotational axis about which the struts will maintain centre locality regardless of the dimensional configuration.

Having created the blue axis it was simply a case of re-introducing the cube and aligning the midpoints of each brown strut with the associated blue reference axis. The image (above left) shows the axis in combination with the cube as a dimetric view and the image on the right shows this in plan.

This image shows everything in combination, quite an overwhelming array of struts!
It would seem in principle that for the majority of “standard” tensegrity structural forms we can derive geometric relationships and symmetry.

The cube, axis of symmetry and star linears are proxy objects, modelled for illustration purposes only. You can see clearly that the axis of symmetry passes through the centre of the brown struts as well as the vertex and centres of the proxy cube elements (green).

Knowing the symmetry and underlying geometry we can define the locations of the actual tensegrity members which is useful as an aid to building a physical tensegrity model or even a 3D CAD model.