Tensegrity: Model Files

I have decided to make available a number of viewable 3D model files from the most recent articles relating to Tensegrity Symmetry.

The link will open a page on Google Docs where the file can be downloaded. Each file created is a 3D PDF which can be viewed in the free Adobe Acrobat Reader. The 3D PDF file format allows the user to interact with the model.

Tensegrity 3v Pars Tetra RS




Tensegrity Cube RS




Tensegrity Tetrahedron RS




Tensegrity T-Prism RS



Tensegrity Octahedron RS




Tensegrity Skew Prism Arch



NOTE: “RS” denotes models inclusive of Axis/Rotational Symmetry elements; in each case the brown struts are the actual tensegrity compression struts, the green and purple struts are virtual elements representing the transitional states and the blue struts are virtual elements to represent the axis of symmetry.

When you “activate” a 3D PDF the file opens with a toolbar across the top of the screen. Some of these files may have been processed as perspective views, so to change this to orthographic just select the toolbar button as highlighted above.
Other toolbar features include lighting setups, rotational and preset views, model hierarchy menu and CAD model presentation options.
If you have any questions about use of these files, viewing options or if you have problems accessing the link, then please drop me a line via the Contact page.

The Google Docs is a temporary location until I find something more permanent.

Tensegrity: T-Prism Geometrix

Considering my current research, it was inevitable that I would have to revisit my earlier theories on the construction of the tensegrity T-Prism and have a look at this structure for rotational symmetry.

http://spatialgeometrix.blogspot.com/2010/09/placeholder-geometry.html

My earlier thoughts on the development of this type of tensegrity still hold true, but building a model based on rotational symmetry has greater appeal and simplicity.

 

 

 

If we consider again the parameters of transition of the morphing from one state to another we will see that the green triangle form transitions to a single linear form as shown on the left image.

The right image (above) shows the relationship of the green triangular form to the blue struts representing the axis of symmetry. These lines intersect on the midpoints of the green struts.

Now we introduce the T-Prism or 3-Prism structure to this assembly and align it accordingly.

The brown struts are located at the midpoint with the blue axis struts resulting in a balanced arrangement.

To create a tapered T-prism move the intersection point of the brown struts towards one end. In each case the brown struts remain perpendicular to the axis of the blue struts.

The last image shows the parallel relationship of all three planes, assuming a plane connecting the triangular arrangement at the top and bottom of the T-prism.

 

 

The concept of rotational symmetry as discussed in the recent posts here is something I am quite excited about.

I would be interested to receive comments on my ideas and hopefully enter into some discussion with others about tensegrity and rotational symmetry.

So please drop me a line at hught2008@gmail.com

Tensegrity: Cube Geometrix

Rotational/Geometric Symmetry; Slowly progressing thru the range of tensegrity structures I have so far modelled it seemed appropriate to now have a look at the cube!

The tensegrity cube featured here is affectionately referred to by Bob Burkhardt as a Zig-Zag cube, somewhat differentiating it from the Orthogonal variant (not shown). This structure in contrast to its cousin has better stability and not quite so “jiggly”. Thus the reason why I am doing this one and not its cousin!

When I started to look for the geometric symmetry in this model I was puzzled as to how this formation could translate from the green cube to the star linear format (purple) as shown in the next 2 images.

 

In combination (above left) the translation formats do little to clarify the situation.

However when I introduced the cube itself into this geometry model I created a third construction set as a reference to represent the axis of geometric symmetry.

The blue axis of symmetry shown below has a common centre point passing through the centre of each strut. Thus we have the rotational axis about which the struts will maintain centre locality regardless of the dimensional configuration.

Having created the blue axis it was simply a case of re-introducing the cube and aligning the midpoints of each brown strut with the associated blue reference axis. The image (above left) shows the axis in combination with the cube as a dimetric view and the image on the right shows this in plan.

This image shows everything in combination, quite an overwhelming array of struts!
It would seem in principle that for the majority of “standard” tensegrity structural forms we can derive geometric relationships and symmetry.

The cube, axis of symmetry and star linears are proxy objects, modelled for illustration purposes only. You can see clearly that the axis of symmetry passes through the centre of the brown struts as well as the vertex and centres of the proxy cube elements (green).

Knowing the symmetry and underlying geometry we can define the locations of the actual tensegrity members which is useful as an aid to building a physical tensegrity model or even a 3D CAD model.

Tensegrity: 3V Pars Tetra

Following on from my last post I decided to revisit some of my earlier models to see how they may also exhibit rotational axis symmetry similar to the truncated tetrahedron.
In this case I selected the 3v Pars Tetra mentioned in one of my first postings:

http://spatialgeometrix.blogspot.com/2010/09/tetrahedron-tensegrity.html

 
I took the original model (left) and inserted a cross axis model; similar to before (blue); aligning the centre line axis with the midpoint of the brown struts in each direction and as you can see we can again show rotational symmetry.

We can also show that if we draw a connecting line between the end points of matching pairs of brown struts that this line should pass thru the centre of the assembly.

Tensegrity: Tetrahedron Geometrix

Introduction to Tensegrity Symmetry: This post has been updated to reflect changes to my blog and was essentially my first study of geometric symmetry.

Bob Burkhardt presented the mathematical formulae to develop this tetrahedron and Marcela Pars also covered this on his website.

It occurred to me that this type of structure must follow some basic rules, so I started looking at proportional geometric relationships for a tetrahedron based on a fixed length of compression strut.

At first my attention was focussed on identifying proportional relationships for the end triangular components for each of the tetrahedron size variants I had already built. I created a circle based on the 3 connection points in each case and then analysed the results. After a great deal of study there was no immediate proportional relationships that could be easily identified.

So I started again this time working from the extremes of tetrahedron displacement. The process is actually quite difficult to explain but I will make an attempt and perhaps follow through later with a more detailed report.

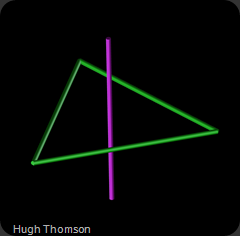
A Tetrahedron in its most basic form is essentially a polyhedron or pyramid shape (above left). The creation of the truncated tetrahedron as we know it is the transition when we morph from the platonic form to a linear form (above right). To better understand this morphing I would refer you to http://complexity.xozzox.de/tensegrity.html, where you can see via the Java applet how the transition works.

The green and blue “struts” are visual reference elements for purposes of clarification and not struts in the sense of being physical components. The blue struts are representative of the linear form which coincidentally also represents an axis had it been projected from the centre of the polyhedron edges to the centroid.

The image above left shows the extreme parameters of the transition from pyramid to linear form. In the image on the right I have introduced a tensegrity tetrahedron to illustrate how the struts splay out creating four triangular truncations. For clarity I have omitted the tendons.

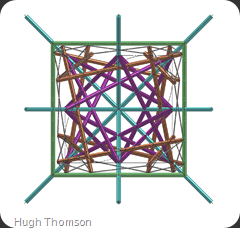
After drawing numerous circles and construction geometries the entire study was becoming very complex and the myriad of lines I had was quite overwhelming, which may explain why I initially missed the most interesting aspect of a tensegrity tetrahedron.

At this stage I had created another tetrahedron with a dimensional variance on the tendons, but still using the same size of strut and placed it into my model..

This is where it started to get interesting as at last a pattern was beginning to emerge!

If you look closely at this image you can see that in each case the brown struts intersect exactly at the midpoint with the blue axis struts (representing the linear extreme parameter).

Essentially the blue struts define an axis of rotational symmetry.

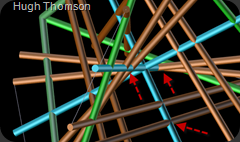
To me my findings are very significant by showing a specific common relationship that ties the struts to a known alignment. I should also note that in each case the brown struts are perpendicular to the blue struts. Please note; it may appear that the same is true for the intersections between the brown struts and the green struts but in fact that is not the case.

So simply by knowing the base geometry and the end linear form geometry we can determine any intermediate location of the struts from the graphical perspective, which ultimately simplifies the modelling; both virtual and physical.

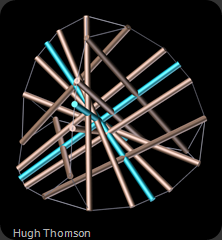
Just to give you some idea of how complex this study got I captured the following image:

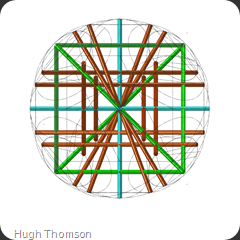
Coincidentally this image also helps to show the strut relationships…the centre intersections and also the perpendicular aspects.

I am not sure if it is very clear, but you may be able to make out the circle perimeter line drawn through the end points of the brown and blue struts that I used to graphically check perpendicularity.

Having now studied in detail the geometry of the T-Prism and the Tetrahedron I am sure that other tensegrity structures may also exhibit some form of physical consistency such that the development of same is much easier to construct and ultimately calculate.

Update: Feb 2012. As this was my first study of Tensegrity Symmetry I have left the post as I wrote it at that time. The process of discovery is typical for a study of this nature concluding that the brown compression struts retain a midpoint relationship perpendicular to a projected axis from the polyhedron to the centroid. The transition to a tensegrity structure maintains this relationship as each strut revolves around this axis.

Thus the term axis/rotational symmetry evolved. At this time having now gained a better understanding of the potential underlying planar geometry pertinent to tensegrity structures I was tempted to rewrite this article but sometimes it is important to record how these discoveries came about.

Tensegrity: Wind Turbine

Is this the worlds first Tensegrity Wind Turbine??
This model combines the membrane Tetrahedron in my last post with the Skylon mast, also described earlier. The big question is “does it work?”

Obviously a model of this nature demands a lot more analysis before it even becomes a viable working design. The mast for example would probably not be sufficient in its current form to be an effective support for the mechanisms required to generate power and I don't have the necessary tools to do a proper design analysis.
However as a simple structure to be moved by the wind the combination I believe would work rather well. I am convinced that there is potential for membrane construction techniques for tensegrity structures and is something I intend to explore further.
Consider for a moment the nature of the membranes in this example. As it turns out they exhibit double curvature properties which is an ideal surface for acting in multi directional airflow situations.


This surface modulation could be enhanced even more by redefining the geometry of the tetrahedron.
hught2008@gmail.com

Tensegrity: Membranes

Having now developed a number of tensegrity structures, based on stick and string or strut and tension designs I decided to have a look at options whereby we replace the tension components with membranes or diaphragms.

I took a fairly common structure known as a truncated tetrahedron and explored a number of variations using membranes.
I should note that the Cad program I use; Soildworks; is not very good at depicting true generation of stressed membranes so the edge curvature is approximated in each case just to give some idea of what it may look like.

Eventually I will try and get hold of an evaluation copy of a membrane design program to test this out to gain a better perspective.

The image on the left assumes a planar arrangement following the route of three continuous tendons and the line of the main connecting strut. I have opted to include a centre connection point on the main strut which resulted in applying a bending force on the strut and needed to be countered by inclusion of the small internal triangular membrane.
The image on the right is a much simpler arrangement essentially following the perimeter of each perceived face of the tetrahedron. As all the points are interconnected there is no requirement to close the triangular end openings.
Kenneth Snelson has a detailed article on triangulated tension networks which could be adapted to develop membrane arrangements.
http://kennethsnelson.net/2010/12-triangulated-tension-networks/
I have no immediate plans to build any of these membrane structures at this time, but again the composite construction technique would be ideal for doing this.

Tensegrity: Skylon Variant

Inspired by the Skylon tower built for the Festival of Britain in 1951. This is also a structure featured by Bob Burkhardt which though similar I have some variance to this design by redefining the geometry with the mast connected midway.








This structure helps to illustrate one of the key advantages of my construction techniques for the compression struts. The concept of composite construction would facilitate a midway connection of the tendons to the vertical strut.

For more information on composite construction please see my earlier post here:
http://spatialgeometrix.blogspot.com/2010/09/tensegrity-concept-models.html

Tensegrity: Skew Prism Arch

My first Tensegrity Arch, inspired by Bob Burkhardt.

This form is known as a Skew Prism Arch, deriving its name from the arrangement of the 3-Prism modules which are skewed along the central axis. The dimensions for this model were governed by the material that I will use to build it, this however imposes a few restrictions resulting in a slight variance in the alignment of the end struts (purple) that otherwise would be exact.

Nevertheless I think it will be a rather nice model to build. I like the symmetry of the structure shown in elevation and the spatial qualities.