Tensegrity: Cube Geometrix

Rotational/Geometric Symmetry; Slowly progressing thru the range of tensegrity structures I have so far modelled it seemed appropriate to now have a look at the cube!

The tensegrity cube featured here is affectionately referred to by Bob Burkhardt as a Zig-Zag cube, somewhat differentiating it from the Orthogonal variant (not shown). This structure in contrast to its cousin has better stability and not quite so “jiggly”. Thus the reason why I am doing this one and not its cousin!

When I started to look for the geometric symmetry in this model I was puzzled as to how this formation could translate from the green cube to the star linear format (purple) as shown in the next 2 images.

 

In combination (above left) the translation formats do little to clarify the situation.

However when I introduced the cube itself into this geometry model I created a third construction set as a reference to represent the axis of geometric symmetry.

The blue axis of symmetry shown below has a common centre point passing through the centre of each strut. Thus we have the rotational axis about which the struts will maintain centre locality regardless of the dimensional configuration.

Having created the blue axis it was simply a case of re-introducing the cube and aligning the midpoints of each brown strut with the associated blue reference axis. The image (above left) shows the axis in combination with the cube as a dimetric view and the image on the right shows this in plan.

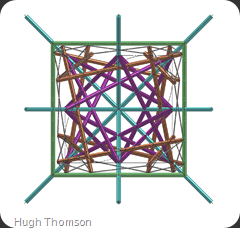
This image shows everything in combination, quite an overwhelming array of struts!
It would seem in principle that for the majority of “standard” tensegrity structural forms we can derive geometric relationships and symmetry.

The cube, axis of symmetry and star linears are proxy objects, modelled for illustration purposes only. You can see clearly that the axis of symmetry passes through the centre of the brown struts as well as the vertex and centres of the proxy cube elements (green).

Knowing the symmetry and underlying geometry we can define the locations of the actual tensegrity members which is useful as an aid to building a physical tensegrity model or even a 3D CAD model.